Probabilistic Hough Transform

In the previous post we discussed Hough Transform and how to implement it to find lines. To get better accuracy we need to compromise on the computing front. It takes a lot of computation power to iterate over all the points and add vote. To reduce this computation, researchers came up with some probabilistic techniques which would increase the computing speed without losing much accuracy.

If we want to detect lines in an input image with M pixels defined as edge points and a parameter space which is devided into N_rxN_Θ accumulators. The computational complexity is O(M.N_Θ) for the voting stage and O(N_r.N_Θ) for the search stage. The complexity and memory requirement drastically increases if we move to higher dimensions.

So to address this problem there a family of algorithms has been developed referred as Probabilistic Hough Transform.

What is Probabilistic Hough Transform

A Hough Transform is considered probabilistic if it uses random sampling of the edge points. These algorithms can be divided based on how they map image space to parameter space.

Probabilistic Hough Transform

One of the easiest probabilstic method is to choose m edge points from the set M edge points. The complexity of the voting stage reduces from O(M.N_Θ) to O(m.N_Θ). This works because a random subset of M will fairly represent the edge points and the surrounding noise and distrotion.

Smaller value of m will result in fast computation but lower accuracy. So the value of m should be appropriately chosen with respect to M.

Kiryati et al performed an analysis which suggested the presence of a thresholding effect for the value of m. Values of m below the threshold gave poor results whilst values above gave very good results. This threshold effect was confirmed experimentally with good results being obtained with as few as 2% of edge points being sampled. However, the value of m must be determined on a per problem basis.

Randomized Hough Transform

Randomized Hough Transform(RHT) uses a many-to-one mapping from image space to parameter space.

From the set of M edge points two points are randomly selected. A line passing through these two points is obtained by solving these equations.

y₁ = ax₁ + b

y₂ = ax₂ + b

This gives a line with parameter (a, b) in parameter space. Now, instead of creating a 2D accumulator array to represent parameter space, a linked list can be used. This list consists of M-2 edge points (We have temporarily removed 2 points). Each point is checked whether it represents (a, b) i.e. whether it lies on the line or not. If a match is found, count of (a, b) is incremented. After each element is processed, the count of (a, b) is stored. 2 points are again randomly selected and this process is repeated.

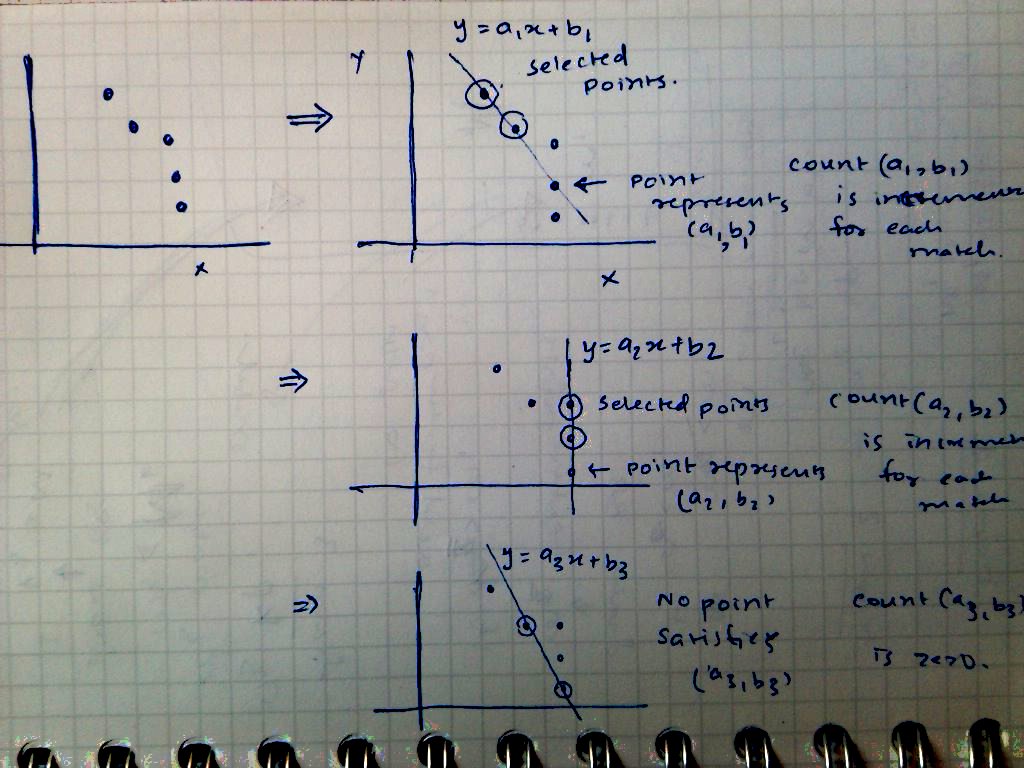
As described in the above image, two out of five points are randomly chosen and parameters (a₁, b₁) are obtained. Point 4 represents (a₁, b₁) and hence its count is increased. When point 2 and point 5 are chosen, we get (a₃, b₃) parameters but no point represents these parameters and hence its count is zero.

This process of selection and removal is repeated. After the process the parameters with high number of votes can be counted as best fit lines.

One complication that arises with this method is that of dealing with tolerances. It is highly unlikely that points will exactly match the given parameters and hence it’s necessary to use some amount of tolerance. If a match within the tolerance is found, the old and new values of (a, b) are averaged and the count is incremented by one.

Advantages

In RHT the storage requirements are greatly reduced and only one accumulator is incremented in each iteration, it is considerably faster than SHT. These improvements have more significance when the dimensionality of parameter space increases.

SHT splits parameter space into descrete space and limits the resolution. The resolution can be increased at the cost of computation. RHT can support high resolution without affecting performance.

Referencs

• Probabilistic Hough Transform

P.S. Added Disqus for comments.

Playing around with Android UI

Articles focusing on Android UI - playing around with ViewPagers, CoordinatorLayout, meaningful motions and animations, implementing difficult customized views, etc.

Read next